The Secret Weapon for Better Equation Discovery: E-graphs and Equality Saturation
This guest post by Fabrício Olivetti de França describes the concepts of Equality Graphs and Equality Saturation and the benefits of using E-Graphs in Symbolic Regression.
In data science, physics, and engineering, the ultimate goal isn't just prediction, it's understanding. Finding a single, elegant mathematical formula that perfectly describes a set of data points is the holy grail. This is called Equation Discovery or Symbolic Regression (SR).
Traditional AI models such as Artificial Neural Networks give us complex, black-box equations. SR aims for human-readable formulas (like $f(x) = \log(x) + c$).
To find this perfect formula, all search algorithms, whether they use Genetic Programming (GP), Monte Carlo Tree Search (MCTS), or Deep Learning (DL), follow a a cycle of: proposing a candidate equation, learning from its performance, and repeat.
How the proposal and learning steps work depends on the algorithm:
- Genetic Programming proposes new equations by modifying existing equations or combining them. It learns by favoring the selection of the best equations found so far.
- Monte Carlo Tree Search proposal step generates a new equation by traversing a tree of possible grammar derivations that are more probable to fit the data taking a confidence interval into consideration. It learns by updating the probabilities of each derivation.
- Deep Learning and Reinforcement Learning proposes new equations by choosing the next symbol that maximizes the expected reward given the last choice. It learns by reinforcing the quality of the generated expression through the sequence of steps.
The problem? The search space is unbelievably vast and filled with redundancy.
It's all the same, no matter where you are
Imagine trying to navigate a forest with many paths leading to the same (wrong) destination, and you have to try them all until you follow one that leads you to your goal. That's the reality of Symbolic Regression. Consider the simple expression $2x$. How many different ways can you write that same value?
$$ x+x \\ \frac{4x}{2} \\ 3x-x \\ \dots \text{and many more!} $$
All these expressions are mathematically identical; they will all yield the exact same result for the same dataset.
This redundancy creates two issues for our search algorithms:
-
Wasted Time: The algorithm might revisit $x+x$ after having already explored $2x$, wasting valuable computational budget.
-
Complexity: If $x+x$ is the correct solution, we want its simplest, and most interpretable form ($2x$), not one of the infinitely complex equivalent forms. Using post-processing simplification tools often fails or introduces new problems, as we've shown in our research [1].
On the other hand, redundancy can be helpful. Sometimes, navigating from $x+x$ to $3x-x$ can be a "stepping stone" to reach a new, better area of the search space. This is known as the neutral space theory [2].
But what if we could detect all equivalent expressions in real-time and use that knowledge to make the search efficient?
A database for math expressions: the E-graph
The solution lies in E-graphs and Equality Saturation [3].
Think of an e-graph as a database for mathematical expressions. It’s designed to store many different, but equivalent, expressions with a minimum amount of space. It also makes it easier to query for expressions with certain patterns.
In an e-graph, symbols (such as $+, -, x, \log$) are called e-nodes. The core concept is the e-class, which acts as an equivalence group. Any e-node belonging to the same e-class represents a mathematically identical value.
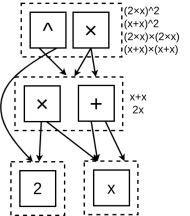
For example, in the figure below, the dashed box in the middle is an e-class. It contains two e-nodes: one for multiplication (2x) and one for addition (x+x). Because they are in the same e-class, the graph automatically knows that $2x = x+x$.

This structure is immensely powerful. Now, when the graph builds a larger expression, such as a term squared (the very top multiplication operator in this e-graph), it knows it can be represented in four different ways instantly:
$$ (2x) (2x) \\ (2x) (x+x) \\ (x+x) (2x) \\ (x+x)(x+x) $$
The E-graph stores all four, but only pays the storage cost for one!
Equality saturation: automatically generating equivalence
How does the E-graph learn what's equivalent? It uses an algorithm called Equality Saturation. This process takes a simple set of mathematical rules (such as the distributive property or $a+a=2a$) and applies them repeatedly until no new equivalences can be found (or until a time limit is reached).
Let’s watch it work on the expression $(x+x)^2$ using three simple rules:
$$ \alpha + \alpha \rightarrow 2\alpha \\ \alpha \times \alpha \rightarrow \alpha^2 \\ \alpha \times (\beta + \gamma) \rightarrow (\alpha \times \beta + \alpha \times \gamma) $$
- Start: Insert $(x+x)^2$ into the graph.
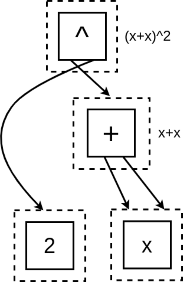
- Apply Rules: The rule $\alpha + \alpha \rightarrow 2\alpha$ applies to the inner expression $x+x$:

- We insert the right-hand side, $2x$ and merge with the e-class for $x+x$, as the graph knows they are identical:

- Repeat until Saturation: The process continues, applying other rules until the E-graph contains every possible equivalent expression derived from these rules:
The most popular implementation of equality saturation is Egg [4], a library written in Rust. But, how can e-graphs and equality saturation help with symbolic regression search?
Symbolic Regression and E-graphs, its a match 💖!
A few years ago, we realized this powerful mechanism could be the missing piece in Symbolic Regression and we pioneered their integration in different applications.
First, we demonstrated that e-graphs are a superior simplification tool compared to standard methods like sympy [1]. By simplifying equations with equality saturation, we not only reduced model complexity but also increased the probability of finding the best-fitting local optima [6].
Second, we found the E-graph structure could be used to analyze how inefficient standard search algorithms like Genetic Programming were under limited budget, showing how often they revisited the same expressions [5] in severly length-limited and therefore constrained search spaces.
At this point, we felt there was much more we could do with e-graphs in SR.
Generating uniqueness
In our most recent work on e-graph genetic programming (eggp) [7], we turned the e-graph into a database and guidance system for equation discovery.
Remember how genetic programming works:
- Create initial random expressions
- Repeat:
- Select two expressions proportional to their performance
- Combine parts of these expressions generating a new expression
- Replace a part of this expression with a random variation
As stated before, this can be inefficient since we can generate many equivalent expressions during the process [5]. But, what if we store every generated expression into a single e-graph and run the equality saturation algorithm?
For once, we would have a database system allowing us to query whether a given expression was already visited, even in an equivalent form. But also, we can use this information to enforce the generation of new expressions!
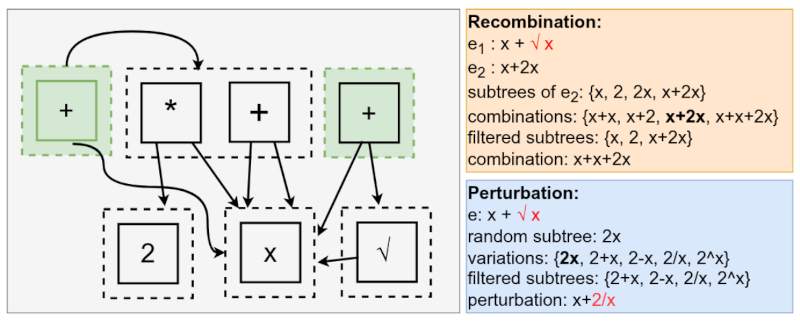
It works like this, imagine that the current state of the search is the e-graph above! The green e-classes are the root of the already evaluated expressions. Let's say that GP decides to recombine the expressions $x + \sqrt{x}$ and $x + 2x$, choosing to replace $\sqrt{x}$ of the first expression with something else from the second. The choices of recombination are ${x+x, x+2, x+2x, x+x+2x}$. We can query each one of these choices to verify whether they already exist in the e-graph. If they do and were already evaluated, we discard them!
Similarly, we can do the same for the mutation. let's suppose we will mutate the expression $x + \sqrt{x}$ by replacing $\sqrt{x}$ with a random expression. If we are unlucky, we may generate the expression $2x$, thus forming $x+2x$, which was already evaluated. After detecting the duplicate, we can change the multiplication in $2x$ with any binary operator that would generate a new expression!
Explore the Search Space with eggp and rEGGression
You can start using this algorithm right now! Here is how you can install our library and use it to find an equation for a real-world fluid dynamics dataset.
You can install eggp with pip:
pip install eggp
Finding a Formula
This example uses eggp to find a relationship for one of the 'Nikuradse problems' [9] (see the tutorials at this link).
from eggp import EGGP
import pandas as pd
pd.set_option('display.max_colwidth', 100)
df = pd.read_csv("datasets/nikuradse_1.csv")
model = EGGP(gen=100, nPop=100, maxSize=15, nTournament=5, pc=0.8, pm=0.2, nonterminals='add,sub,mul,div,power,exp,log', loss='MSE', simplify=True, dumpTo='regression_example.egg')
model.fit(df[['r_k', 'log_Re']], df['target'])
print(model.results[['Expression', 'loss_train', 'loss_val', 'size']])
After running the search, the final e-graph (stored in regression_example.egg) contains the entire history of visited, unique solutions. This can be used to resume the search with different settings, such as a different nonterminal set:
model = EGGP(gen=100, nPop=100, maxSize=15, nTournament=5, pc=0.8, pm=0.2, nonterminals='add,sub,mul,div,power,exp,log,sin,tanh', loss='MSE', loadFrom='regression_example.egg')
model.fit(df[['r_k', 'log_Re']], df['target'])
print("\nLast population resumed from the first Pareto front: ")
print(model.results[['Expression', 'loss_train', 'loss_val', 'size']])
Interactive Model Selection with rEGGression
This e-graph can be further explored with the rEGGression tool [8]. An e-graph explorer for Symbolic Regression.
from reggression import Reggression
egg = Reggression(dataset="datasets/nikuradse_1.csv", loadFrom="regression_example.egg", loss="MSE")
print(egg.top(5, pattern="v0 ^ v0")
This will retrieve the top 5 expressions that follow the pattern $\alpha^\alpha$, such as $x^x$ or $\log((x+5)^{x+5}) + 3$. The result is a list of the best-performing models matching your structural criteria:
| Expression | Fitness | Size |
|---|---|---|
| $\left({\operatorname{log}({\log_{Re}^{\log_{Re}}})^{\theta_{0}}} \cdot r_{k}\right)^{\theta_{1}}$ | -0.001514 | 10 |
| $\left(\left({\log_{Re}^{\log_{Re}}} \cdot \theta_{0}\right) + \frac{\theta_{1}}{\operatorname{log}(r_{k})}\right)$ | -0.001567 | 10 |
| $\left(\frac{\operatorname{log}({\log_{Re}^{\log_{Re}}})}{\left(\theta_{0} \cdot r_{k}\right)} + \theta_{1}\right)$ | -0.004623 | 10 |
| $\left(\frac{\left(r_{k} + \theta_{0}\right)^{\theta_{1}}}{\operatorname{log}(r_{k})^{\operatorname{log}(r_{k})}} + \theta_{2}\right)$ | -0.005701 | 13 |
| $\left(\operatorname{log}({\log_{Re}^{\log_{Re}}}) \cdot r_{k}\right)^{\theta_{0}}$ | -0.010011 | 8 |
Or retrieving the top-5 expressions not having the pattern $\log(v)$:
print(egg.top(5, pattern="log(v0)", negate=True)
| Expression | Fitness | Size |
|---|---|---|
| $\left(\left( \left(\theta_{0} \cdot r_{k}\right)^{\theta_1 ^ {\log_{Re}}} \cdot \theta_{2}\right) + \theta_{3} \right)$ | -0.001131 | 11 |
| $\left({\left(\log_{Re} \cdot \theta_{0}\right)^{\theta_{1}}} \cdot \left(r_{k} + \theta_{2}\right)\right)^{\theta_{3}}$ | -0.001187 | 11 |
| $\left(\frac{\left(r_{k} + \theta_{0}\right)^{\theta_{1}}}{\left(\frac{\theta_{2}}{log_{Re}} + \theta_{3}\right)} + \theta_{4}\right)$ | -0.001190 | 13 |
| $\left({\left(e^{\left(\log_{Re} + \theta_{0}\right)} \cdot \theta_{1}\right)^{\theta_{2}}} \cdot r_{k}\right)^{\theta_{3}}$ | -0.001191 | 12 |
| $\left(\theta_0 \cdot \left(\left(\left(\log_{Re} \cdot \log_{Re}\right) \cdot \theta_{1}\right) + r_{k}\right)\right)^{\theta_{2}}$ | -0.001192 | 11 |
Conclusion
The integration of e-graphs and equality saturation is not just an academic exercise; it's a fundamental change in how we approach Symbolic Regression. By treating equivalent expressions as one, we eliminate computational waste and focus the search entirely on finding novel and better solutions.
Our eggp algorithm shows the potential of this integration, achieving state-of-the-art results with a streamlined genetic programming framework. Furthermore, rEGGression gives the human expert unparalleled power to explore the results, acting as an interactive tool for guided model selection that is agnostic to the original SR method.
The days of algorithms driving in circles are over. E-graphs have provided the GPS.
Coming up Next!
This library is not limited to just that! In the next blog post we will show how to use rEGGression to integrate and improve other algorithms!
Technical Details
Our e-graph implementation is available at the Haskell Symbolic Regression library with some differences from egg to make it more convenient for symbolic regression and memory efficient.
Our SR algorithm eggp already shows the potential of this integration, being capable of beating the state-of-the-art with a simple genetic programming framework.
The rEGGression Python library make it easy to explore the explored solutions and can be used as an interactive tool for a guided model selection.
References
[1] de Franca, Fabricio Olivetti, and Gabriel Kronberger. "Reducing overparameterization of symbolic regression models with equality saturation." Proceedings of the Genetic and Evolutionary Computation Conference. 2023.
[2] Banzhaf, Wolfgang, Ting Hu, and Gabriela Ochoa. "How the combinatorics of neutral spaces leads genetic programming to discover simple solutions." Genetic Programming Theory and Practice XX. Singapore: Springer Nature Singapore, 2024. 65-86.
[3] Tate, Ross, et al. "Equality saturation: a new approach to optimization." Proceedings of the 36th annual ACM SIGPLAN-SIGACT symposium on Principles of programming languages. 2009.
[4] Willsey, Max, et al. "Egg: Fast and extensible equality saturation." Proceedings of the ACM on Programming Languages 5.POPL (2021): 1-29.
[5] Kronberger, Gabriel, et al. "The inefficiency of genetic programming for symbolic regression." International Conference on Parallel Problem Solving from Nature. Cham: Springer Nature Switzerland, 2024.
[6] Kronberger, Gabriel, and Fabricio Olivetti de Franca. "Effects of reducing redundant parameters in parameter optimization for symbolic regression using genetic programming." Journal of Symbolic Computation 129 (2025): 102413.
[7] de França, Fabrício Olivetti, and Gabriel Kronberger. "Improving Genetic Programming for Symbolic Regression with Equality Graphs." Proceedings of the Genetic and Evolutionary Computation Conference. 2025.
[8] de França, Fabrício Olivetti, and Gabriel Kronberger. "rEGGression: an Interactive and Agnostic Tool for the Exploration of Symbolic Regression Models." Proceedings of the Genetic and Evolutionary Computation Conference. 2025.
[9] Guimerà, Roger, et al. "A Bayesian machine scientist to aid in the solution of challenging scientific problems." Science Advances Vol. 6, No. 5, eaav6971, doi: 10.1126/sciadv.aav69 2020.